Probability Calculator

This calculator can calculate the probability of two events, as well as that of a normal distribution.
Also, learn more about different types of probabilities.

Single Event Probability
Number of possible outcomes: Number of events occured:

Result

Probability of event that occurs P(A): Probability of event that does not occurs P(A'):
Multiple Event Probability
Number of possible outcomes: Number of event occurs in A: Number of event occurs in B: Note: A & B are mutually exclusive events

Result

P(A):
P(A'):
P(B):
P(B' ):
P(A ∩ B):
P(A ∪ B):
P(A | B):
  • See More Tools
    • If you use this great tool then please comment and/or like this page.
    Average Rating:     Tool Views: 2.3k

    Is this tool helpful?
    How can we improve it?

    Subscribe for Latest Tools


    How to use this Probability Calculator Tool?

    How to use Yttags's Probability Calculator?

    • Step 1: Select the Tool
    Probability Calculator Step 1
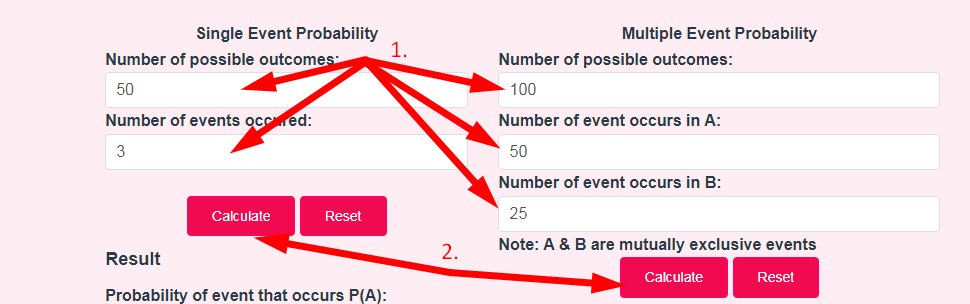
    • Step 2: Enter Number of possible outcomes & Number of events occured And Click On Calculate Button
    Probability Calculator Step 2
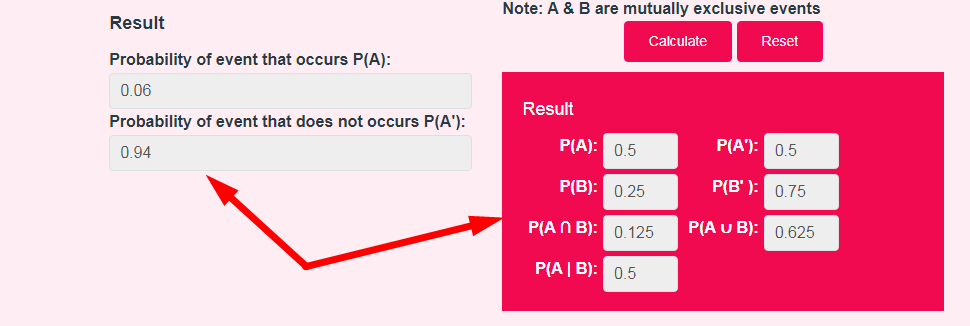
    • Step 3: Check Your Probability Calculator Result
    Probability Calculator Step 3

    Use the probability calculator to find the likelihood of various interactions between two distinct events.


    If you want to link to Probability Calculator page, please use the codes provided below!

    Probability Calculator

    FAQs for Probability Calculator

    What is a Probability Calculator?
    A Probability Calculator is a tool that computes the likelihood of an event or outcome occurring based on given inputs or distributions. It is commonly used in statistics and probability theory to analyze and predict the chances of different events.
    How probability is calculated?
    To calculate probability, you must divide the number of favorable events by the total number of possible events. This generates a sample, and the calculation can be performed from the data obtained.
    What probability rule is needed to calculate the probability?
    That is, if event A is made up of possibilities B and C, then the probability of A is equal to the probability of B+C. So, P ( A ) = P ( A ⋂ B ) + P ( A ⋂ C ) . An alternative to this formula is P ( A ) = P ( A | B ) ⋅ P ( B ) + P ( A | C ) ⋅ P ( C ) .
    What is the addition rule for probability calculator?
    When calculating the probability of either one of two events from occurring, it is as simple as adding the probability of each event and then subtracting the probability of both of the events occurring: P(A or B) = P(A) + P(B) - P(A and B)
    Why is probability important?
    Probability provides information about the likelihood that something will happen. Meteorologists, for instance, use weather patterns to predict the probability of rain. In epidemiology, probability theory is used to understand the relationship between exposures and the risk of health effects.