Convolution calculator
Discover the formula and learn how to calculate convolution effortlessly with our handy calculator. Simplify your math tasks today!
If you use this great tool then please comment and/or like this page.
Average Rating: Tool Views: 429
Average Rating: Tool Views: 429
Subscribe for Latest Tools
How to use this Convolution calculator Tool?
How to use Yttags's Convolution calculator?
- Step 1: Select the Tool
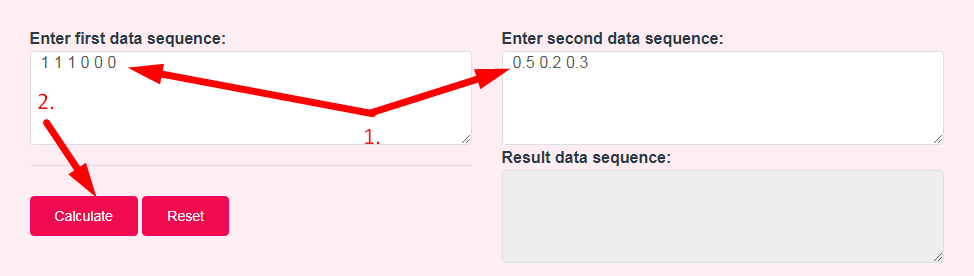
- Step 2: Enter first data sequence: & Enter second data sequence: And Click On Calculate Button
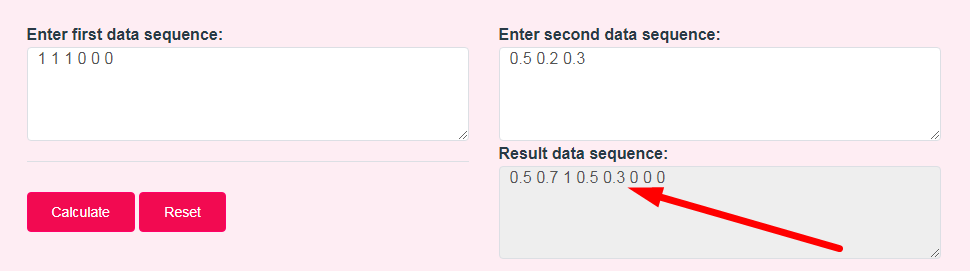
- Step 3: Check Your Convolution calculator Result
An online calculator that calculates the convolution of two sequence, produces Z-Transform transfer function of the impulse and frequency response.
If you want to link to Convolution Calculator page, please use the codes provided below!
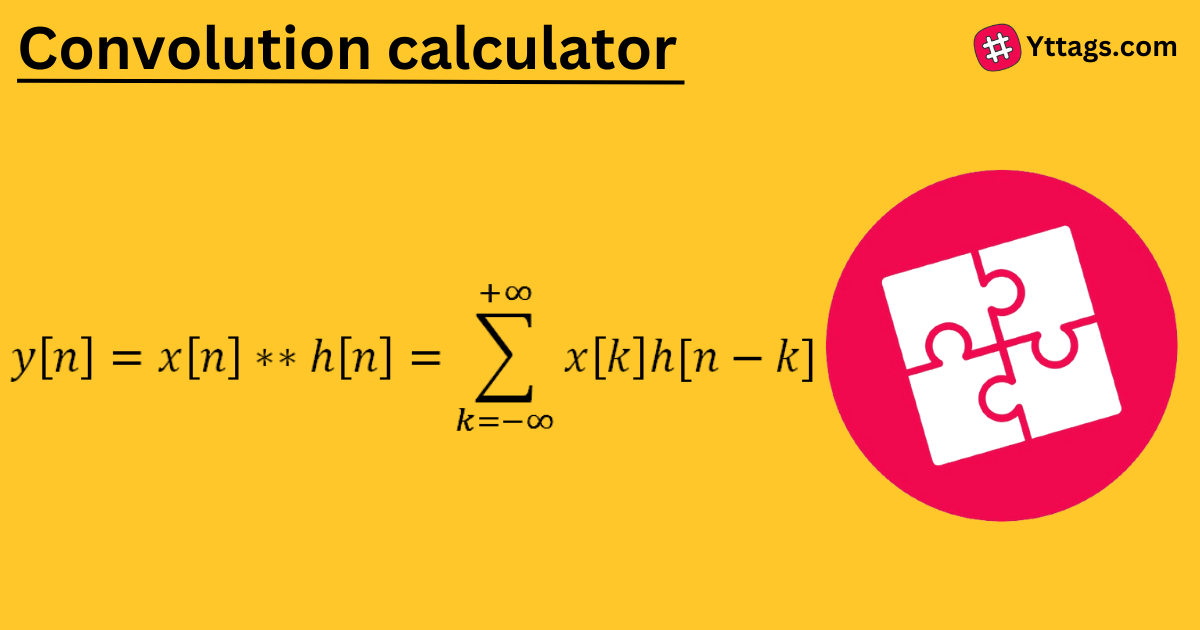
FAQs for Convolution calculator
What is a Convolution calculator?
A Convolution calculator is a tool used to perform mathematical operations known as convolutions, combining two functions to produce a third. In signal processing and image analysis, convolutions are employed to blend or filter data, and these calculators help simplify the computational process.
What is the main purpose of convolution?
Convolution is used in the mathematics of many fields, such as probability and statistics. In linear systems, convolution is used to describe the relationship between three signals of interest: the input signal, the impulse response, and the output signal.
What is convolution in real life?
Convolution has applications that include probability, statistics, acoustics, spectroscopy, signal processing and image processing, geophysics, engineering, physics, computer vision and differential equations. The convolution can be defined for functions on Euclidean space and other groups (as algebraic structures).
What are the properties of convolution?
, Convolution is a linear operator and, therefore, has a number of important properties including the commutative, associative, and distributive properties.
Why is convolution better?
Convolutional neural networks work because it's a good extension from the standard deep-learning algorithm. Given unlimited resources and money, there is no need for convolutional because the standard algorithm will also work. However, convolutional is more efficient because it reduces the number of parameters.