Power Set Calculator
Power Set An online calculator for kids and students. Find the powerset for a given set step-by-step
Enter Set Value separate with comma
Power Set Definition
The Power Set (P)
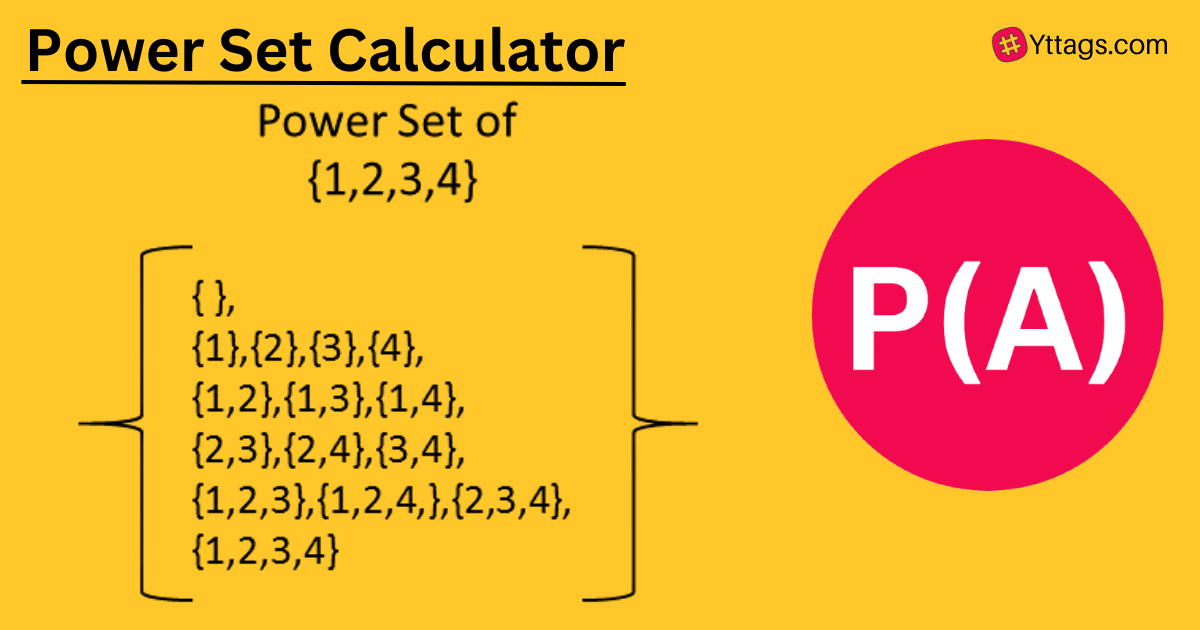
The power set is the set of all subsets that can be created from a given set.
ExampleA=(0,1,2)
P(A) = {},{0},{1},{2},{0,1},{0,2},{1,2},{0,1,2}
The power set of A is all subsets of A
If you use this great tool then please comment and/or like this page.
Average Rating: Tool Views: 380
Average Rating: Tool Views: 380
Subscribe for Latest Tools
How to use this Power Set Calculator Tool?
How to use Yttags's Power Set Calculator?
- Step 1: Select the Tool

- Step 2: Enter Set Value separate with comma And Click On The Calculate Button.

- Step 3: Check Your Power Set Calculator Result

If you want to link to Power Set Calculator page, please use the codes provided below!
FAQs for Power Set Calculator
What is a Power Set Calculator?
A Power Set Calculator is a mathematical tool or program that generates all possible subsets of a given set, including the empty set and the set itself. It's commonly used in combinatorics and computer science for tasks like permutation and combination calculations.
How do you check if a set is a power set?
Step 1: Find the member of x that itself contains the most elements, in this case {1, 2} . If there is more than one possibility, then x is not a power set. Step 2: The power set of {1, 2} is {{1, 2}, {1}, {2}, {}} , call this 'y'. Step 3: x is a power set only if x = y .
How do you calculate the size of a power set?
For a given set S with n elements, number of elements in P(S) is 2^n. As each element has two possibilities (present or absent}, possible subsets are 2×2×2.. n times = 2^n. Therefore, power set contains 2^n elements.
How do you find the number of sets in a power set?
The total number of subsets for a set of 'n' elements is given by 2n. Since the subsets of a set are the elements of a power set, the cardinality of a power set is given by |P(A)| = 2. Here, n = the total number of elements in the given set. |P(A)| = 2n = 22 = 4.
Can a set be equal to its power set?
If Power Set has any elements, since Power Set definitely has empty set , There never exist any finite set which equals its own Power Set. The only I have considered is that empty set.